참고 자료
유투브 쉬운코드 functional dependency 함수 종속
Functional Dependency (FD)
한 테이블에 있는 두 개의 attribute(s) 집합 사이의 제약

EMPLOYEE 테이블
집합 X: empl_id
집합 Y: empl_name, birth_date, position, salary
두 tuple의 X 값이 같다면 Y 값도 같다
empl_id는 EMPLOYEE 테이블의 각 튜플을 unique하게 식별할 수 있는 PK 이다.
X 값에 따라 Y 값이 유일하게 결정될 때
X가 Y를 함수적으로 결정한다(functionally determine)
Y가 X를 함수적으로 의존한다(functionally dependent)
두 집합 사이의 이러한 제약 관계를 functional dependency(FD)라고 부른다
X → Y
Functional Dependency (FD) 파악하기
테이블의 스키마를 보고 의미적으로 파악해야 한다
즉, 테이블의 state를 보고 FD를 파악해서는 안된다

테이블을 Messi ~ Joy 까지 조회하면 empl_name → birth_date FD가 존재한다고 생각할 수 있지만
Jinho 이름은 또 존재 가능하다.
즉, 테이블의 특정 순간의 특정 상태(state)만 보고 FD가 존재한다고 생각하면 안된다
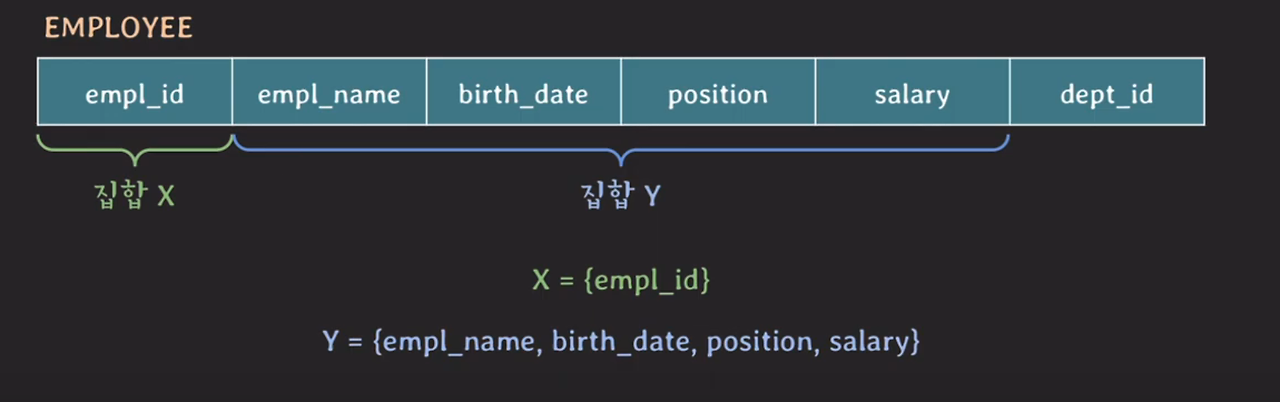
현재 FD에서 Y에 dept_id는 빠져있다.
이건 회사 정책에 따라 달라진다.
만약 임직원은 하나의 부서에만 속할수 있다라는 제약이 있으면
X → Y FD에 dept_id 도 포함된다.
하지만 임직원이 여러 부서에 속할 수 있다면 dept_id는 포함되서는 안된다.
Functional Dependency (FD) 예시
{student_id} → {student_name, birth_date, address}
{class_id} → {class_name, year, semester, credit}
{student_id, class_id} → {grade}
{bank_name, bank_account} → {balance, open_date}
Functional Dependency (FD) 특징
X → Y 가 반드시 Y → X 도 성립한다?
성립할 수도 있고 아닐 수도 있다. 케이스 바이 케이스
학번 → 이름 / 이름 → 학번? X
학번 → 주민등록번호 / 주민등록번호 → 학번 O
X → Y 일관성
input(X)가 같으면 항상 output(Y)가 같다.
{} → Y
특정 attribute(s)에 따라서 달라지는 게 아닌 어떤 값을 넣어도 동일한 결과가 나오는 케이스

{} → {company}
Functional Dependency (FD) 종류
trivial FD
when X → Y holds, if Y is subset of X, then X → Y is trivial FD
{a,b,c} → {c}
{a,b,c} → {a,c}
{a,b,c} → {a,b,c}
non-trivial FD
when X → Y holds, if Y is NOT subset of X, then X → Y is non-trivial FD
{a,b,c} → {b,c,d}
{a,b,c} → {d,e} is non-trivial FD & completely non-trivial FD (겹치는 attribute(s)가 하나도 없다. )
Partial FD
proper subset
집합 X의 proper subset은 X의 부분 집합이지만 X와 동일하지는 않은 집합
예를 들어, X = {a,b,c}일 때
{a,b},{a},{}는 모두 X의 proper subset 이다
{a,b,c}는 X의 proper subset이 아니다
partial FD
when X → Y holds, if any proper subset of X can determine Y, then X → Y is partial FD
when {empl_id, empl_name} → {birth_date} holds,
because {empl_id} can determine {birth_date}, then this FD is partial FD
Full FD
when X → Y holds, if every proper subset of X can NOT determine Y, then X → Y is full FD
when {student_id, class_id } → grade(성적) holds,
beacuse {student_id}, {class_id}, {} can NOT determine {grade}, then this FD is Full FD
'DataBase' 카테고리의 다른 글
| [DB] 파티셔닝, 샤딩, 레플리케이션 (0) | 2024.11.16 |
|---|---|
| [DB] B tree 전체 정리 (0) | 2024.11.15 |
| [DB] DB 정규화 (0) | 2024.11.15 |
| [DB] 테이블 설계의 중요성 (2) | 2024.11.14 |
| [WINDOW] PostgreSQL 설치 (0) | 2024.09.03 |



