Algorithm [Math] 코딩 테스트에서 나오는 수학 개념 정리

https://www.youtube.com/watch?v=2RCJApSVxRI&list=PLtqbFd2VIQv4O6D6l9HcD732hdrnYb6CY&index=19

목차

1. 소수

2. 약수

3. 최대공약수 

4. 최소공배수 

5. 연립합동방정식

6. 이항 계수 

소수

소수의 정의 

소수 = 1과 자기 자신으로만 나누어지는 수 / 약수가 2개인 수 

      

합성수 = 1과 자기 자신을 제외한 다른 약수를 가지고 있는 수 

 

주의!  1은 소수도 합성수도 아니다.

 

소수 판정법

2부터 N-1까지의 수로 나누어지지 않는 수

 

간단하게 소수를 판정하는 메서드 

    public boolean isPrime(int n){
        if(n == 1) return false;
        for(int i = 2; i < n; i++){
            if(n % i == 0) return false;
        }
        return true;
    }

 

2 ~ N - 1까지 N이 나누어지는지 확인한다.

시간 복잡도 : O(N)

 

시간 복잡도를 O(√N)으로 확인하는 방법

 

합성수 N에서 1을 제외한 가장 작은 약수는 √N 이하이다. 

N = 18 : 2 <= √18 

N = 25 : 5 <= √25  

N = 21 : 3 <= √21

 

2부터 N-1 까지 수를 나누어서 소수임을 판정하는 대신에 

√N 까지만 나누어보면 소수임을 판정이 가능하다.

    public boolean isPrime2(int n){
        if(n == 1) return false;
        for(int i = 2; i * i <= n; i++){
            if(n % i == 0) return false;
        }
        return true;
    }

 

여기서 Math.sqrt(n)을 사용하지 않고 i * i 를 사용하는 이유는 Math.sqrt는 실수 연산이기 때문에 오차의 범위가 있다. 

그래서 i * i의 정수 연산을 사용한다.

 

관련 문제 백준 1978: 소수 찾기 

https://20240228.tistory.com/78

[Java] [Math] 백준 1978 소수 찾기 브론즈2

 

이렇게 어떤 수 하나가 소수인지 O(√N)에 판단하는 방법을 익혔다. 

만약 1부터 N까지의 모든 수에 대해 그 수가 소수인지 판단하는 알고리즘이 필요하면 어떤 방식으로 구현을 해야 할까?

가장 간단한 방법은 각 수가 소수인지 구하는 작업을 매번 반복하면 된다. 

 

범위 내에서의 소수 판정법 - 에라토스테네스의 체

 

1부터 N까지의 소수의 목록을 구하고 싶을 때 이렇게 N칸짜리 배열을 만든다. 

이 배열은 해당 칸의 수가 소수일 경우 true, 소수가 아닌 경우 false의 값을 가진다. 

그림에서는 파란색이 true, 빨간색이 false이다. 

 

커서를 하나 둬서 2를 가리키게끔 한다. 이 커서는 2부터 N까지 진행하면서 소수를 찾은 후에 뭔가 작업을 할 거다. 

 

2는 내버려두고 2의 배수를 전부 false로 만든다. 4, 6, 8 ..... 

다음으로 커서를 다음 칸으로 옮긴다. 

 

현재 커서는 3을 가리키고 있다. 

 

3도 파란 칸 즉 소수니까 3은 빼고 다른 3의 배수들을 false로 만든다. 

 

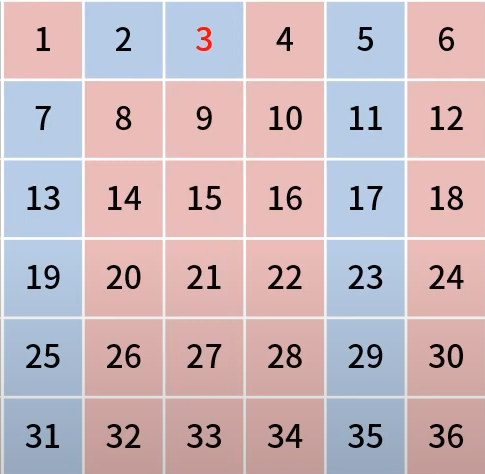
커서를 다음 칸으로 옮긴다. 이번에 4인데 4는 현재 빨간 칸이다. 그러면 4는 소수가 아니라는 의미이기 때문에 그냥 넘어간다. 그 다음은 5이다. 5는 파란 칸이니 소수여서 5의 배수들을 false로 만든다. 커서가 N에 도달할 때까지 지금 작업을 계속 반복하면 된다. 그럼 최종적으로는 이렇게 소수만 파란색으로 남는다. 

 

 

이렇게 마치 체로 곡식을 거르는 것 처럼 합성수를 제거해나가는 알고리즘을 에라토스테네스의 체라고 부른다.

 

구현 코드 

public class SieveOfEratosthenes {
    public static void main(String[] args) {
        int n = 40;
        boolean [] memo = new boolean[n+1]; // false : 소수 true : 합성수 

        for (int i = 2; i <= n; i++) {
            if(memo[i]) continue;
            for(int j = 2; i * j <= n; j++){
                memo[i * j] = true;
            }
        }
        StringBuilder sb = new StringBuilder();
        for (int i = 2; i <= n; i++) {
            if(!memo[i]) sb.append(i).append(" ");
        }
        System.out.println(sb);
    }
}

 

출력 

2 3 5 7 11 13 17 19 23 29 31 37

 

지금 이 코드는 수학적으로 개선이 필요할 수 있는 부분이 있다. 

어떻게 개선할까?

 

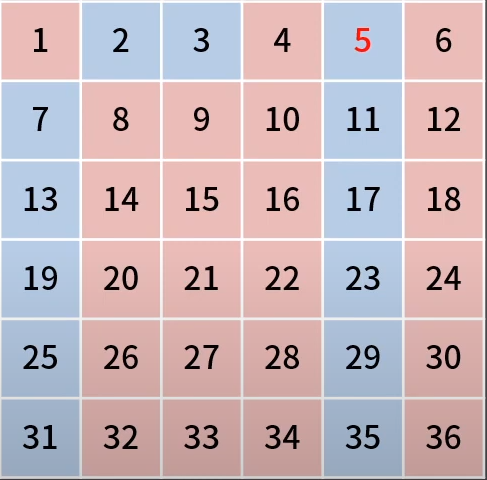
그림에서 나타내고 있는 상황에서는 커서가 5을 가리키고 있고 5의 배수인 10, 15, 20, 25, 30, 35를 false로 만들 차례이다. 그런데 이 5의 배수들을 보면 이미 합성수로 판정이 되어있는 값들이 많다. 25, 35만 아직 true이고 나머지는 다 false이다. 

현재 커서는 5에 있다. 그러면 커서는 2와 3을 거쳐왔고 자연스럽게 5보다 작은 소인수를 가지는 합성수는 이미 다 걸려졌다. 

25 보다 작은 5의 배수를 보면 10 = 2 * 5, 15 = 3 * 5, 20 = 4 * 5이다. 예네들은 각각 2, 3, 4로 나누어 떨어지고, 이들은 5보다 더 작은 소인수가 존재한다는 의미이다. 그래서 우리는 5^2 = 25부터 false로 바꿔나가면 된다. 

 

구현 코드 

public class SieveOfEratosthenes {
    public static void main(String[] args) {
        int n = 40;
        
        StringBuilder sb2 = new StringBuilder();

        boolean [] memo2 = new boolean[n+1];
        for (int i = 2; i <= n; i++) {
            if(memo2[i]) continue;
            sb2.append(i).append(" ");
            for(int j = i * i; j <= n; j += i){
                memo2[j] = true;
            }
        }

        System.out.println(sb2);
        
    }
}

 

출력 

2 3 5 7 11 13 17 19 23 29 31 37

 

최종 시간 복잡도 O(NloglogN)

 

관련 문제 : 백준 1929: 소수 구하기  

https://20240228.tistory.com/79

[Java] [Math] 백준 1929 소수 구하기 실버3

 

소인수 분해

소인수분해 : 정수를 소수의 곱으로 나타내는 것을 의미한다. 

ex) : 1100 = 2 * 2 * 5 * 5 * 11 

 

cur : 1100

target : 2 

 

1. cur % target == 0  cur /= target  소인수 목록에 target을 넣는다. 

2. cur % target != 0   cur++

 

1, 2번을 반복 

 

시간 복잡도 : O(N)

 

시간 복잡도를 O(√N)으로 개선이 가능하다. 

소수 판정하는 알고리즘이랑 똑같다. 

 

구현  코드

public class Factorization {
    public static void main(String[] args) {
        int target = 999;
        ArrayList<Integer> list = new ArrayList<>();
        for (int i = 2; i * i <= target; i++) {
            while (target % i == 0){
                list.add(i);
                target /= i;
            }
        }
        if(target != 1) list.add(target);
        System.out.println(list);
    }
}

 

관련 문제 : 백준 11653 소인수 분해 

https://20240228.tistory.com/80

[Java] [Math] 백준 11653 소인수 분해 브론즈1

약수

약수 : 어떤 수를 나누어 떨어지게 하는 수 

18의 약수 = 1, 2, 3, 6, 9, 18 

 

i = 1 부터 √N 까지 N % i == 0 이라면 약수 리스트에 넣는다 대신 (제곱수) N / i == i 라면 1번만 넣는다. 

 

구현 코드

// 약수
public class Divisor {
    public static void main(String[] args) {
        int target = 18;
        ArrayList<Integer> list = new ArrayList<>();
        for (int i = 1; i * i <= target; i++) {
            if(target % i != 0) continue;
            int temp = target / i;
            if(temp != i){
                list.add(temp);
                list.add(i);
            }
            else list.add(i);
        }
        Collections.sort(list);
        System.out.println(list);

        list.clear();
        target = 16;
        for (int i = 1; i * i <= target; i++) {
            if(target % i != 0) continue;
            int temp = target / i;
            if(temp != i){
                list.add(temp);
                list.add(i);
            }
            else list.add(i);
        }
        Collections.sort(list);
        System.out.println(list);
    }
}

 

출력 

[1, 2, 3, 6, 9, 18]
[1, 2, 4, 8, 16]

 

최대공약수

최대공약수(Greatest Common Divisor) = 두 자연수의 공통된 약수 중 가장 큰 약수 

 

20의 약수 = 1, 2, 4, 5, 10, 20 

12의 약수 = 1, 2, 3, 4, 6, 12      

 

GCD(20, 12) = 4 

 

유클리드 호제법 

두 수 A, B에 대해 A를 B를 나눈 나머지를 r이라고 하면 GCD(A, B) = GCD(B, r)이다. 

 

GCD(20, 12) = GCD(12, 8) =  GCD(8, 4) =  GCD(4, 0) =  4

 

구현 코드 

public class GCD {
    public static void main(String[] args) {
        int A = 20; int B = 16;
        System.out.println(GCD(A, B));
    }
    public static int GCD(int a, int b){
        if(b == 0) return a;
        return GCD(b, a % b);
    }
}

 

출력 : 4 

 

최소공배수 

최소공배수 : Least Common Multiple(LCM)

 

A * B = GCD(A, B) * LCM(A, B)

LCM(A, B) = (A * B) / GCD(A, B) 

 

구현 코드 

public class LCM {
    public static void main(String[] args) {
        int A = 20; int B = 16;
        System.out.println(LCM(A,B));
    }
    public static int LCM(int a, int b){
        return a * b / GCD(a, b);
    }
    public static int GCD(int a, int b){
        if(b == 0) return a;
        return GCD(b, a % b);
    }
}

 

출력 : 80

연립합동방정식

민경 선생님은 자신의 반 학생이 몇 명인지 갑자기 기억이 나지 않았다. 다만

- 6명씩 조를 짰을 때 3명이 남았다. 

- 5명씩 조를 짰을 때 2명이 남았다. 

- 학생은 30명 미만이다. 

 

이 3가지 사실은 기억하고 있다. 민경 선생님의 반 학생들은 몇 명일까?

 

정리 

N % 6 = 3

N % 5 = 2

N < 30

 

가장 간단한 방법 : for문을 통해서 i = 0 ~ 29 까지 해당 조건이 맞는 학생수를 찾기 더 효율적인 방법을 생각해 보자

 

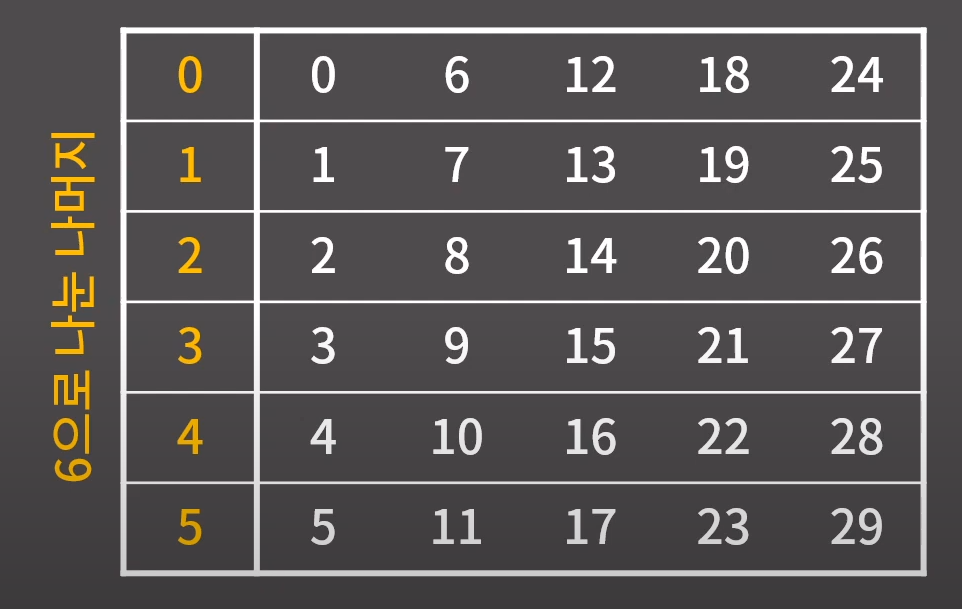
6으로 나누면 나머지가 3인 값들을 먼저 뽑고 해당 값들 중에 5로 나누면 나머지가 2인 값을 찾는다. 

 

for문 범위가 0 ~ 29에서 0, 9, 15, 21, 27 -> 5개로 줄었다.

 

관련 문제 : 백준 6064 카잉 달력

https://20240228.tistory.com/81

[Java] [Math] 백준 6064 카잉 달력 실버1

이항계수

 

순서를 고려하지 않고 뽑는 경우의 수 = 조합

순서를 고려해 뽑는 경우의 수 = 순열 

 

관련 문제 : 백준 11050 이항 계수 1

https://20240228.tistory.com/82

[Java] [Math] 백준 11050 이항 계수 브론즈1

 

관련 문제 : 백준 11051 이항 계수 2

 

이항 계수 1 문제와 다르게 이항 계수 2 문제는 n, k가 엄청 크다. 자바 long 타입으로도 해결 불가능 

이 식을 가지고 DP를 통해서 해결 

DP[i][j] = DP[i-1][j] + DP[i-1][j-1]

https://20240228.tistory.com/83 

[Java] [Math] 백준 11051 이항 계수 2 실버2