https://school.programmers.co.kr/learn/courses/30/lessons/258711
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
코딩테스트 연습 > 2024 KAKAO WINTER INTERNSHIP > 도넛과 막대 그래프
문제 설명
도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프들이 있습니다. 이 그래프들은 1개 이상의 정점과, 정점들을 연결하는 단방향 간선으로 이루어져 있습니다.
크기가 n인 도넛 모양 그래프는 n개의 정점과 n개의 간선이 있습니다. 도넛 모양 그래프의 아무 한 정점에서 출발해 이용한 적 없는 간선을 계속 따라가면 나머지 n-1개의 정점들을 한 번씩 방문한 뒤 원래 출발했던 정점으로 돌아오게 됩니다. 도넛 모양 그래프의 형태는 다음과 같습니다.

크기가 n인 막대 모양 그래프는 n개의 정점과 n-1개의 간선이 있습니다. 막대 모양 그래프는 임의의 한 정점에서 출발해 간선을 계속 따라가면 나머지 n-1개의 정점을 한 번씩 방문하게 되는 정점이 단 하나 존재합니다. 막대 모양 그래프의 형태는 다음과 같습니다.

크기가 n인 8자 모양 그래프는 2n+1개의 정점과 2n+2개의 간선이 있습니다. 8자 모양 그래프는 크기가 동일한 2개의 도넛 모양 그래프에서 정점을 하나씩 골라 결합시킨 형태의 그래프입니다. 8자 모양 그래프의 형태는 다음과 같습니다.

도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프가 여러 개 있습니다. 이 그래프들과 무관한 정점을 하나 생성한 뒤, 각 도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프의 임의의 정점 하나로 향하는 간선들을 연결했습니다.
그 후 각 정점에 서로 다른 번호를 매겼습니다.
이때 당신은 그래프의 간선 정보가 주어지면 생성한 정점의 번호와 정점을 생성하기 전 도넛 모양 그래프의 수, 막대 모양 그래프의 수, 8자 모양 그래프의 수를 구해야 합니다.
그래프의 간선 정보를 담은 2차원 정수 배열 edges가 매개변수로 주어집니다.
이때, 생성한 정점의 번호, 도넛 모양 그래프의 수, 막대 모양 그래프의 수, 8자 모양 그래프의 수를 순서대로 1차원 정수 배열에 담아 return 하도록 solution 함수를 완성해 주세요.
제한 사항
1 ≤ edges의 길이 ≤ 1,000,000
edges의 원소는 [a,b] 형태이며, a번 정점에서 b번 정점으로 향하는 간선이 있다는 것을 나타냅니다.
1 ≤ a, b ≤ 1,000,000
문제의 조건에 맞는 그래프가 주어집니다.
도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프의 수의 합은 2이상입니다.
문제 접근
예제1

예제1에서 추가된 정점을 어떻게 찾을 수 있을까?
현재 그래프에서는 정점2가 추가된 정점이다.
추가된 정점은 다음 2가지 특징을 가진다.
indegree 가 0이다.
indegree가 정확한 표현인진 모르겠는데 들어오는 간선의 개수를 indegree로 표현한다.
2번 정점과 4번 정점은 현재 indegree가 0이다.
그럼 2번 정점과 4번 정점중에 어떤 정점이 추가된 정점일까? 간선의 개수가 더(제일) 많은게 추가된 정점이다.
예제2

똑같이 예제2에서도 추가된 정점을 찾아보자.
예제2에서는 indegree가 0인 정점은 4밖에 없다. 그래서 4번 정점이 추가된 정점이다.
이렇게 쉽게 추가된 정점을 구했다.
실제로는 여러 시행착오로 나온 결과이긴 하다.. ㅠ
각 그래프는 특징을 가진다.
정점의 개수와 간선의 개수가 같으면 도넛 모양
정점의 개수보다 간선의 개수가 1 작으면 막대 모양
정점의 개수보다 간선의 개수가 1 크면 8자 모양
각 그래프의 특징도 다 구했고 그래프의 개수를 찾아야 하는데 어떻게 찾을까?
우린 이미 추가된 정점을 구했다.
이걸 통해 손쉽게 다른 그래프들을 구하는 게 가능하다.
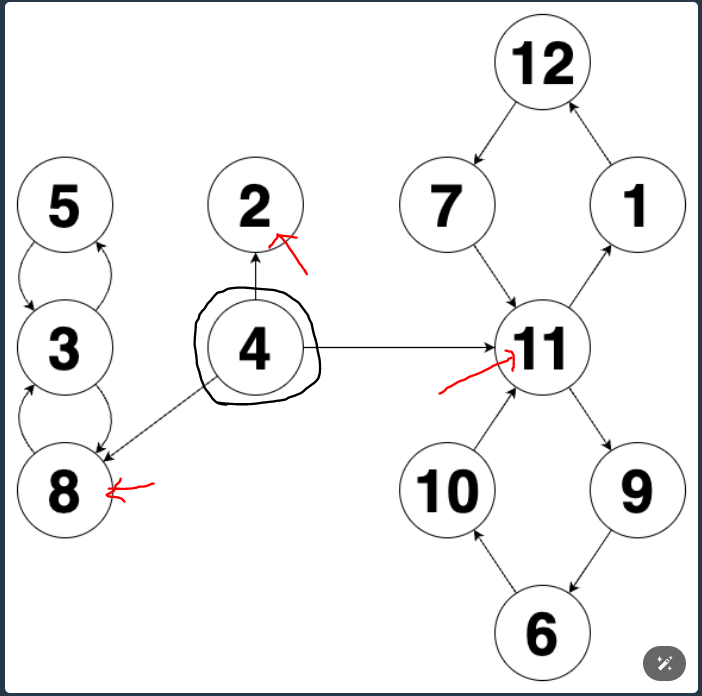
추가된 정점의 간선들로 연결된 8,2,11을 각 그래프의 시작 정점으로 두고 그래프 탐색을 하면서
각 그래프의 정점의 개수, 간선의 개수를 구하면 그래프 모양을 구할 수 있다.
이제 전체 코드를 보자
전체 코드
import java.util.*;
class Solution {
public int[] solution(int[][] edges) {
int [] answer = new int [4];
int max_v = 0;
for(int i = 0; i < edges.length; i++){
max_v = Math.max(max_v, Math.max(edges[i][0], edges[i][1]));
}
ArrayList<Integer>[] graph = new ArrayList[max_v+1];
for(int i = 0; i <= max_v; i++){
graph[i] = new ArrayList<>();
}
int [] indegree = new int [max_v+1];
for(int i = 0; i < edges.length; i++){
graph[edges[i][0]].add(edges[i][1]);
indegree[edges[i][1]]++;
}
int v = 0;
int max = 0;
for(int i = 1; i<= max_v; i++){
if(indegree[i] != 0) continue;
// 간선이 가장 많으면서 들어오는 간선이 없는 정점 찾기
// 해당 정점이 추가된 정점
if(graph[i].size() > max){
v = i;
max = graph[i].size();
}
}
answer[0] = v; // 추가된 정점 answer 기록
// ArrayDeque는 시작과 끝의 삽입 삭제가 많은 경우
// 시간복잡도 상에서 링크드 리스트 보다 유리하다.
ArrayDeque<Integer> ad = new ArrayDeque<>();
// 그래프의 개수는 추가된 정점의 간선의 개수와 동일하다.
boolean [] visited = new boolean[max_v+1];
for(int i = 0; i < graph[v].size(); i++){
// start는 각 그래프의 리프 노드
// 모든 간선을 돌면서 정점의 개수와 간선의 개수를 기록하자
int start = graph[v].get(i);
int n = 1; // 정점의 개수
int c = 0; // 간선의 개수
visited[start] = true;
ad.addLast(start);
while(!ad.isEmpty()){
int cur = ad.pollFirst();
int size = graph[cur].size();
c += size; // 간선의 개수 추가
for(int j = 0; j < size; j++){
int next = graph[cur].get(j);
if(visited[next]) continue;
visited[next] = true;
n++; // 정점의 개수 추가
ad.addLast(next);
}
}
if(n == c) answer[1]++; // 도넛 모양
else if(n - 1 == c) answer[2]++; // 막대 모양
else answer[3]++; // 8자 모양
}
return answer;
}
}
왜 그래프 탐색에서 일반적으로 사용하는 Queue를 사용하지 않고 ArrayDeque라는 다소 생소한 자료구조를 사용했을까?
궁금하시면 깃허브 링크를 참고해 주세요
https://github.com/jeus1998/About-Java/blob/main/record/LinkedList%20vs%20ArrayDeque.md
읽어주셔서 감사합니다!
'Algorithm > Programmers Java' 카테고리의 다른 글
| [JAVA] 프로그래머스 level2 [PCCP 기출문제] 2번 / 석유 시추 (0) | 2024.06.21 |
|---|---|
| [JAVA] 프로그래머스 level3 주사위 고르기 (0) | 2024.06.19 |
| [Java] 프로그래머스 level3 입국심사 (0) | 2024.05.17 |
| [Java] 프로그래머스 level3 스티커 모으기(2) (0) | 2024.05.03 |
| [Java] 프로그래머스 level3 거스름돈 (1) | 2024.04.28 |

